Graph Ranking - part 3
Posted on 17/08/2021 by Roberto Cornacchia
In the first and the second part of this blog mini-series about graph ranking we have used a small subset of our graph: only nodes of type Movie, ranked by some of their properties. It is also possible, and most useful, to rank nodes of some class based on the relevance of some different but related classes.
Ranking across multiple node classes
As an example, let's rank movies by their title and by the user reviews they received. This time, the review text is not a direct property of a Movie node, but a property of a Review node. The two are connected via an edge labelled "has_review".
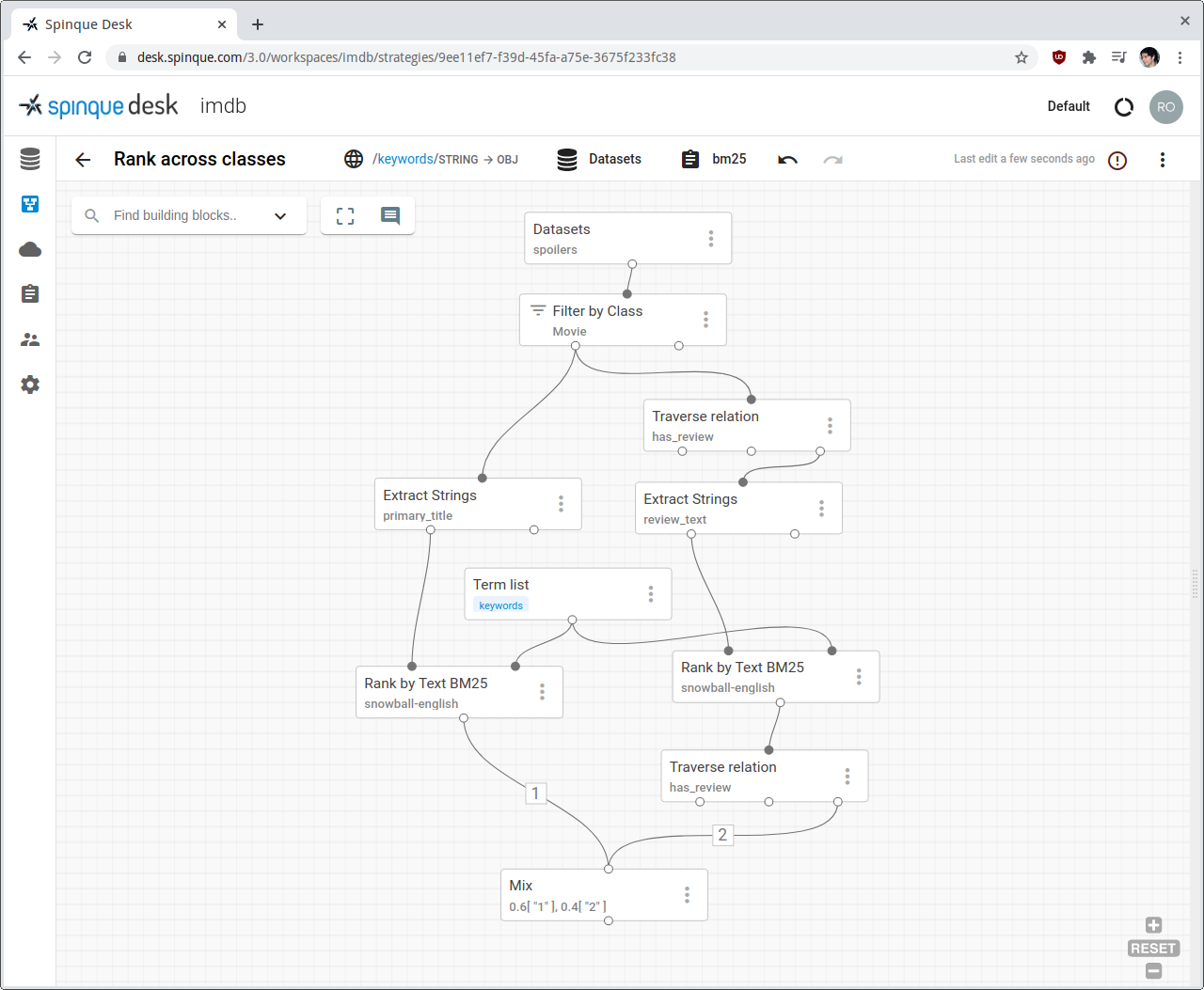
In the screenshot, the left branch of the strategy ranks movies by their titles, as usual. The right branch does something different: it ranks reviews and propagates their scores to the respective movies. The first Traverse Relation block has movie nodes in input and traverses the edges starting from them that are labelled "has_review". This operation effectively returns all the reviews by traversing all triples (movie,has_review,review) in the database.
For the daring reader
Traversing edges is one of the most important graph operations. Given a set of nodes in input, block Traverse Relation reaches all nodes that are connected via a specific edge label, also called the predicate.
Graph edges are directed and their predicate normally indicates the intended natural forward direction: predicate has_review implies edges connecting movies to reviews, with an arrow pointing to reviews, or, in triple representiation, (Movie "X", has_review, Review "Y"). When moving from reviews in input to movies in output, we will need to traverse this relation backwards.
In most cases, configuring block parameters Predicate and Direction is all that is needed. The block has however a few more parameters.
- Parameter Use sub-predicates. As introduced in Part 1, blocks involving classes and properties can optionally consider the sub-classes and sub-properties of those configured in the block. The same applies to predicates and sub-predicates. As an example, the IMDB graph could include predicates has_user_review and has_critic_review, both defined as sub-predicates of has_review. Using this option in conjunction with predicate has_review, one could traverse both sub-relations at once.
- Parameter Minimum/Maximum number of steps. Sometimes it is useful to traverse the same relation multiple times. Think for example of a graph describing social media, with users linked by a friend_of relation. Requesting more than 1 traversal step allows to collect all friends, friends of friends, and so on, until the desired degree of friendship.
- Parameter Step weight. Used in conjunction with the previous setting, it allows to apply an increasing penalty at every traversal step. In the social media example, indirect friendships would be considered less relevant than direct friendships.
- Parameter Score Aggregation is present in almost all blocks and it has to do with duplicates in the result sets. The same node could be retrieved via different paths in the sub-strategy preceding the current block, thus with different scores. We can then choose to keep all the duplicates, or to keep only the one with maximum or minimum score, for example.
- Parameter Score Normalisation is present in many blocks and can be used to normalise the final scores, in case previous operations made them unsuitable to be interpreted as probabilities (e.g. Parameter Score Aggregation = SUM resulting in scores greater than 1).
- Parameter Normalise over entire graph. Related to Score Normalisation, which by default only considers the result set of the block to find the MAX/MIN/SUM/.. used in the normalisation operation. When this option is checked, the entire graph is considered instead. This yields more smoothened normalisations, in case the block result set contains extremely frequent or infrequent items.
Reviews are then ranked by their review_text property, just as we did with movies so far. The last important step is to traverse the graph back from reviews to movies (we do expect movies in the final result). We do this by using again block Traverse Relation configured for traversing edge "has_review". However, this time we change the parameter Direction from its default Forward to Backward, which starts from reviews and yields movies when processing triples (movie,has_review,review).
How did ranking reviews and then going back to movies help us rank movies? It helps because Spinque graphs are supported by probabilistic database operations. All the operations that we can perform on a graph update and propagate the probabilities attached to every bit of evidence across nodes, properties, and edges. When we traverse edge has_review backward from reviews to movies we are actually asking: given these reviews with their probabilities (of relevance to our query), what is the probability of the connected movies? We do not need to compute those probabilities ourselves, the engine does that continuously, under the hood.
Ranking across edges
Another way of ranking graph nodes is by measuring how they are connected in the graph. For example, to get a ranked list of the most reviewed movies, we can count the edges between nodes of types Movie and Review, and use this count for estimating each movie's probability of relevance.
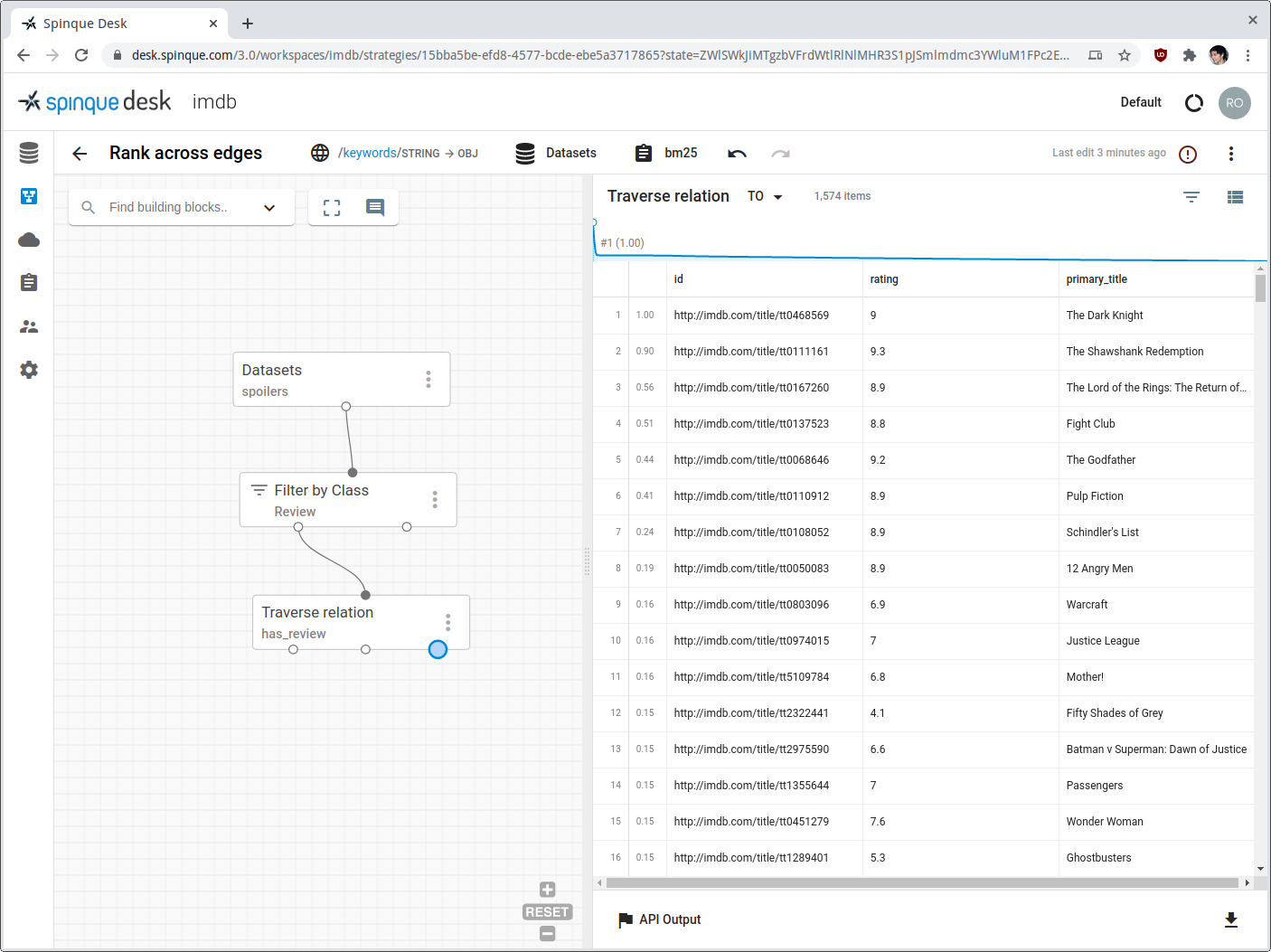
We do that by using the aggregation function in the Traverse Relation block. Let's start from all nodes of type Review. From there, we traverse backwards the "has_review" edges to the movies the reviews are about. Because each movie can have several reviews, this traversal operation will produce several instances of the same movie in the result.
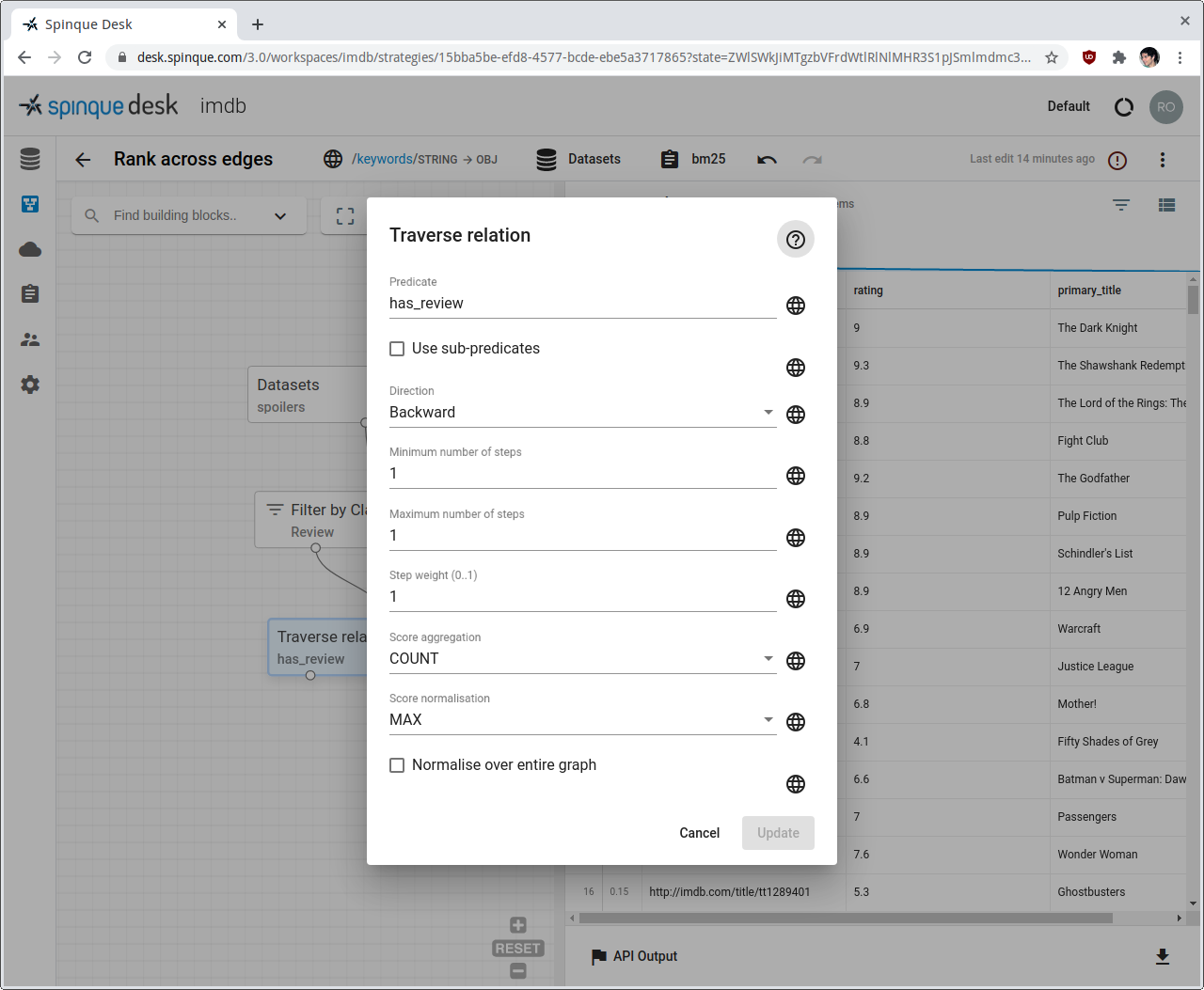
The default setting for parameter Score aggregation in the Traverse Relation block is MAX, which de-duplicates results by keeping in this case only the movie instance with maximum score.
In order to count edges, we set:
- Score aggregation = COUNT
- Score normalisation = MAX
This will normalise the per-movie review counts to a score between 0 and 1, which the system will interpret again as a probability of relevance.
This type of ranking is often used to establish a prior probability which relates to concepts such as authoritativeness, reliability, or interest in general. Here we have used it to indicate that the more reviews a movie received, the more attention it got and therefore the more potentially relevant it is, regardless of any other search criteria.
We can use the same type of prior assignment between users and reviews by counting the edges of triples (user, made_review, review), to indicate that users who have written more reviews tend to be more knowledgeable / reliable. Therefore, that not all reviews have the same importance.
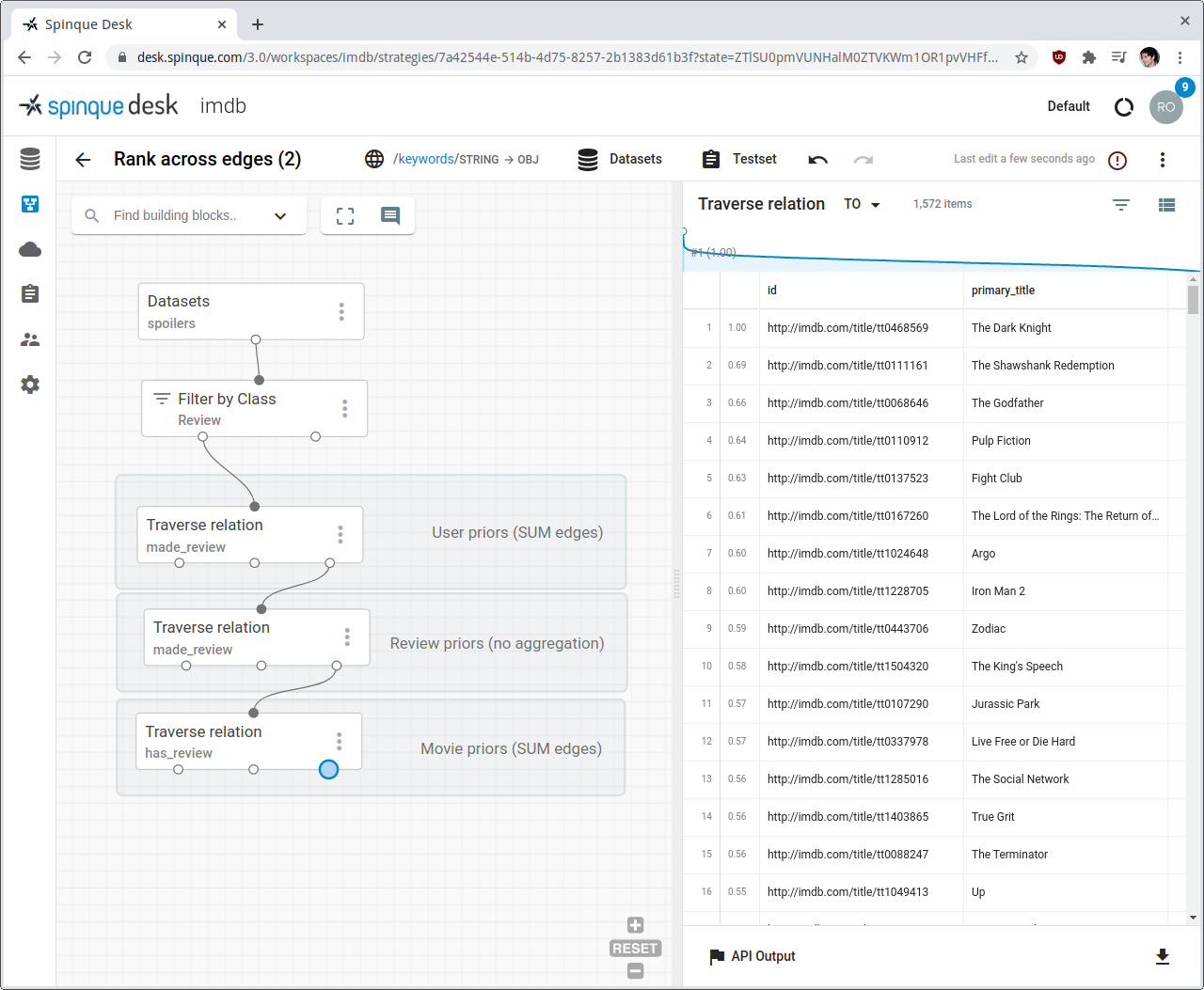
Once we have ranked users by reliability, we can transfer those priors to reviews written by them, by simply traversing the corresponding edges.
Now that we have ranked reviews, we can use an improved version of our initial prior assignment to movies. Instead of simply counting the reviews that each movie received, we are going to take into account the reviews' priors that we have just learned.
Since each review's prior now has a value between 0 and 1 we are going to use Score aggregation = SUM instead of Score aggregation = COUNT.
A more realistic movie search
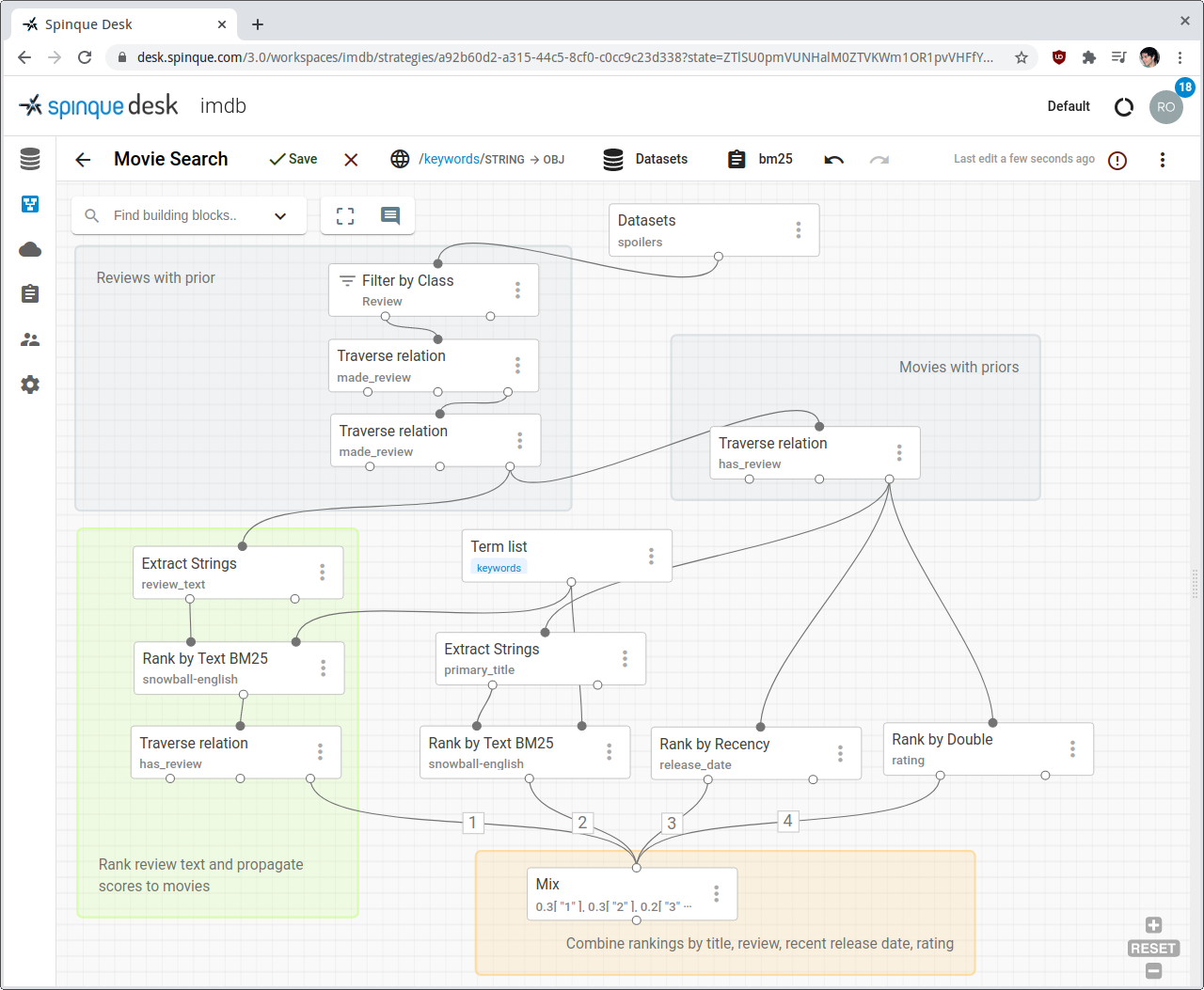
We can now put together all the small patterns that we have seen so far, as in the strategy depicted in the last screenshot. We can also use annotations (the coloured boxes) to help us remember the role of each smaller part in the whole strategy.
The gray boxes assign priors to users, reviews and movies, by summing the contribution of edges connected to each node. These ranked nodes will be used as the input for subsequent ranking operations, thus propagating the priors learned so far.
The three rankings without a coloured box are directly performed on movie properties (of types text, double, date).
The green box ranks reviews by text and propagates their scores to the respective movies, inducing a ranking on them.
Finally, the Mix block in the orange box creates a final ranking by linearly interpolating all the rankings created so far.
This post concludes the mini-series dedicated to Graph Ranking. We have explored approaches that go from simple attribute ranking, to combining relevance evidence in several ways, to end with relevance propagation throughout the graph.
I hope that you found it useful and that it can inspire you in your next search strategy creations. Above all, I hope I have convinced you that probabilistic knowledge graphs offer ways of expressing your own concept of relevance that go well beyond a few pre-cooked text-ranking algorithms.